Starting with client version 1.12 the user can enter a PIN which is hashed and sent to the server. This post details how the client calculates the hash for World of Warcraft 1.12 and provides replication values in order to test your own implementation.
Background
The server may send a PIN grid seed and PIN salt in CMD_AUTH_LOGON_CHALLENGE_Server
wiki
if it chooses.
The client may send the PIN salt and client PIN hash in CMD_AUTH_LOGON_PROOF_Client
wiki
in the field just after the client proof.
Figure 1 shows the PIN window during login.
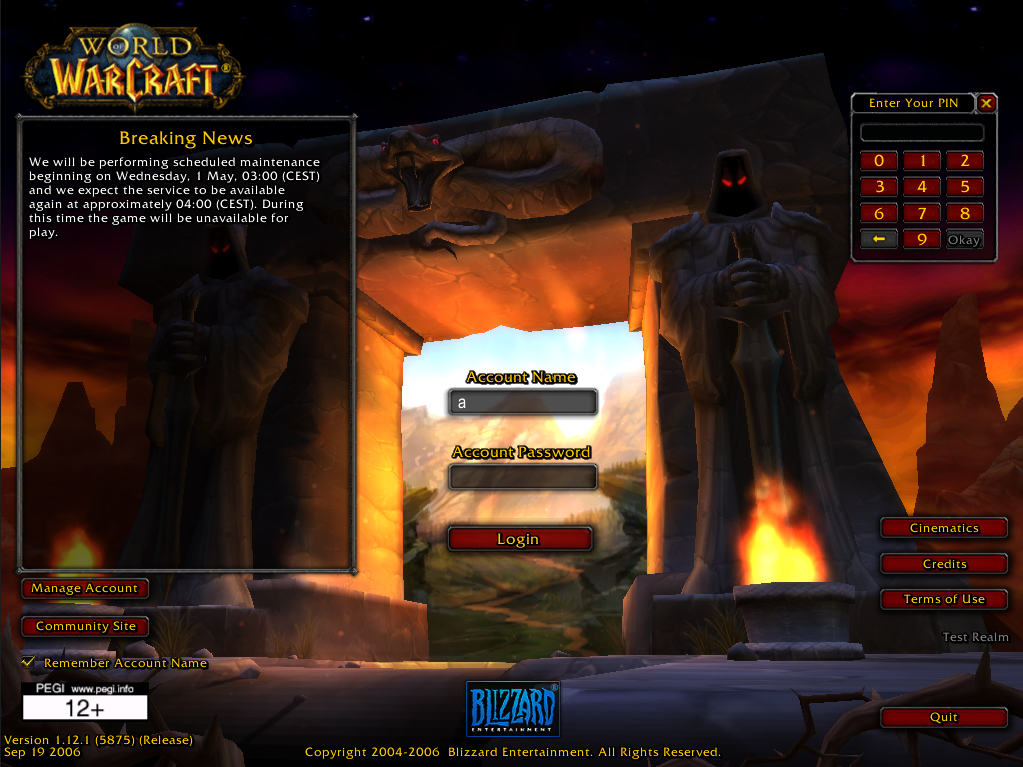
The client does not require the server to prove that expected key matches like it does for the primary authentication check.
This will work for all versions after 1.12.
The PIN the client enters can either be a static (it never changes) or be time based, the client just sends the digits entered by the user.
PINs can be between 4 and 10 digits long.
The implementation is the same for the server and client. They will both calculate a hash for the entered digits and the server will then compare the two hashes for equality.
The grid of the PIN can be randomized with the PIN grid seed sent by the server.
This will move the locations of the numbers so that they are no longer in order.
So instead of the keypad being 1, 2, 3, ..., it could be 9, 2, 5, ....
Figure 2 shows the randomized PIN window.

Implementation details
The algorithm goes through the following steps:
- Get the PIN from the client or database.
- Use the PIN grid seed to randomize the grid.
- Apply the randomized grid to the PIN.
- Convert PIN to ASCII by adding
0x30(48) to every value. - The PIN is SHA1 hashed twice along with server and client salts.
The PIN is in the form of a byte array of at least 4 bytes and at most 10 bytes, where every byte is a single digit of the PIN.
So a PIN of 1, 2, 3, 4 would be an array of [1, 2, 3, 4].
Main Algorithm
This function ties everything together.
pinis the digits of the PIN code as a byte array.pin_grid_seedis the PIN grid seed.server_saltis the salt sent by the server.client_saltis the salt sent by the client.%is the modulus operator.+is array concatenation.SHA1is the SHA1 hash function.
function calculate_hash
argument pin: array of bytes
argument pin_grid_seed: u32
argument server_salt: array of 16 bytes
argument client_salt: array of 16 bytes
returns array of 20 bytes
remapped_pin_grid = remap_pin_grid(pin_grid_seed)
randomized_grid = randomize_grid(pin, remapped_pin_grid)
# Convert to ASCII
for b in randomized_grid:
b += 0x30
first_hash = SHA1(server_salt + randomized_grid)
return SHA1(client_salt + first_hash)
Implementations
Verification values
pin | pin_grid_seed | server_salt | client_salt | expected |
|---|---|---|---|---|
| Big Endian Hex | Unsigned integer | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Remap PIN Grid
This function converts the PIN grid seed into a remapped array.
pin_grid_seedis sent by the server inCMD_AUTH_LOGON_CHALLENGE_Server.%is the modulus operator.
function remap_pin_grid
argument pin_grid_seed: u32
returns array of 10 bytes
grid = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
remapped_grid = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
# Go backwards
# Start on 10 and do not go to 0
for i in 10..0:
# Iteration count, could also use enumerate()
remapped_index = 10 - i
remainder = pin_grid_seed % i
pin_grid_seed = pin_grid_seed / i
remapped_grid[remapped_index] = grid[remainder]
copy_size = i - remainder - 1
for j in 0..copy_size:
grid[remainder + j] = grid[remainder + j + 1]
return remapped_grid
Implementations
Verification values
pin_grid_seed | expected |
|---|---|
| Unsigned integer | Big Endian Hex |
Randomize Grid
This function converts the PIN grid seed into a remapped array.
bytesis the PIN as a byte array.remapped_pin_gridis the remapped PIN grid created byremap_pin_grid.
function randomize_grid
argument bytes: array of bytes
argument remapped_pin_grid: array of 10 bytes
# Can return a new array if modifying bytes in place is not possible
for i, byte in enumerate(bytes):
remapped_value = index of byte value from remapped_pin_grid
bytes[i] = remapped_value
Implementations
Verification values
bytes | remapped_pin_grid | expected |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |