The authentication protocol for authenticating with a World of Warcraft (WoW) server is widely available but not very well documented. Most documentation is spread across forums or just directly links to RFC2945, the 8 page, 20 year old, very broad and unspecific RFC that describes SRP6 in relatively academic terms.
The goal of this article is to be an approachable, complete guide to implementing the protocol specifically for WoW 1.12 without requiring external references.
The article starts out by giving a high level overview of the protocol and the specifics of the WoW implementation before giving a function-by-function implementation guide, including files for verification and examples of implementation in Rust, C++ and Elixir.
Important terms have been highlighted with bold. The exact definitions of these will come later in the article.
This article will only cover the SRP6 protocol, not the network aspects of authenticating with a client.
This is not intended to be a guide for production usage. I have no cryptographic experience and essentially stumbled upon the solutions by accident. SRP6 is also not very widely used, possibly for a reason. Use this only for interacting with legacy World of Warcraft game clients.
Ensure that you actually need to implement this from scratch
There is little reason to implement this from scratch if you can just use an existing library for it.
These are the libraries that I know of, if you want yours added to the list send me an email. There are more implementations linked later in the article, but they are part of applications and can’t be used as libraries.
| Name and link | Author | Language | Comment |
|---|---|---|---|
| wow_srp | Gtker | Rust | |
| wow_srp_python | Gtker | Python | Python bindings to wow_srp. |
| wow_srp_csharp | Gtker | C# | Native .NET Standard 2.1 compatible. |
| wow_srp_c | Gtker | C/C++ | C/C++ bindings to wow_srp. |
| wow_srp6 | oiramario | Python | Native Python implementation. |
| go-wow-srp6 | Kangaroux | Go | Native Go implementation. |
SRP6 Overview
SRP6 is a protocol for proving that a client and server both know the same specific password without having to send it over the network. It does this via various mathematical tricks, none of which are important to us.
When a new account is added, the server generates a random salt value and calculates a password verifier before saving the username, salt and password verifier to the database.
When authenticating, the protocol works in 5 different stages:
- The client sends their username to the server.
- The server retrieves the password verifier and salt from the database, then it randomly generates a private key which it uses to calculate a public key. It then sends the public key and salt to the client, as well as a large safe prime and a generator.
- The client generates a private key and calculates a public key. Then it calculates a session key and client proof. It then sends both the public key and client proof to the server.
- The server calculates a session key, then calculates the client proof on its own and compares it to the one the client sent. If they are identical the client and server have used the same password for their calculations. The server then sends a server proof to the client to prove that it also knows the correct password.
- If the client gets an identical server proof it is now authenticated and will send the “Send Realmlist” packet to ask the server to send a realmlist.
- If the client loses connection, it can reconnect by proving that it knows the original session key. More on this in the Reconnecting section.
The above description can also be seen as a sequence diagram in figure 1.
PlantUML Source
There are some important conceptual points to remember:
- The private keys are never sent over the network. Only the client will know what the client private key is, and only the server will know what the server private key is. Both values are chosen completely at random and are not identical.
- The public keys are sent over the network and are not identical.
- The session keys are calculated by both the client and the server based on different variables. These keys are identical and the client proof and server proof prove to the other part that they both have the same session key without saying what the key is.
- The client proof and server proof are calculated using the public information and their respective session keys. This means that the client calculates a client proof, then the server calculates a client proof using the same algorithm and if the client proofs match the session keys used are identical. The same happens for the server proofs.
Reconnecting and packet header encryption are described in their own sections.
Important Knowledge Before Starting
Before we dive into the implementation itself, there are a few things you should know that would ease your implementation.
Integers
You will need to convert an array of bytes to a number, this is often called a BigInt, BigInteger or arbitrary size integer.
You might need a third party library for this although some languages do have standard library support for this.
The integers should be signed and positive.
Modulo vs Remainder
It’s important that your BigInteger implementation uses modulo rather than the remainder for mod_pow.
With remainder, (-2)^3 % 9 = -8 while with modulo (-2)^3 % 9 = 1.
Test your BigInteger implementation and if it uses remainder, add the large safe prime to the result to get the correct result.
For example:
large_safe_prime = 9
a = -2
b = 3
result = a.mod_pow(b, large_safe_prime)
# if result == 1 you don't need to do anything else
# if result == -8 you need to create a wrapper around your mod_pow like so:
def real_mod_pow(a, b, large_safe_prime):
c = a.mod_pow(b, large_safe_prime)
if c < 0:
c += large_safe_prime
return c
result = real_mod_pow(a, b, large_safe_prime)
# result is now 1
Convertion of hexadecimal strings to byte arrays
When using the provided examples you will need to convert a hexadecimal string to arrays of bytes. It’s important to understand the difference between a byte array of a hexadecimal integer, and a byte array of a string.
Hexadecimal strings can be thought of as containing a byte every 2 characters.
So the string FF would be an array with a single element containing the value 255 (0xFF), while the string FFEE would be an array with two elements containg the value 255 (0xFF) and the value 238 (0xEE).
A byte array of a string are the literal values that represent the characters in the string, while a byte of array of an integer are the individual components of the integer.
So the byte array of the hexadecimal string FF would contain two elements with the value 70 (0x46) and the value 70, since these are the ASCII/UTF-8 values of the F character.
Consider two the functions HexToBytes and StringToBytes.
HexToBytes converts a hexadecimal string to an array of the byte values while StringToBytes converts any string to an array of the character values.
If you read one of the examples and get the hexadecimal string ABCDEF you can test whether you have a byte array of the string or the byte values by checking the length of the returned by array.
The array returned by HexToBytes for the string ABCDEF would contain 3 elements ([ 0xAB, 0xCD, 0xEF ]), while the array returned by StringToBytes for the string ABCDEF would contain 6 elements ([ 0x41, 0x42, 0x43, 0x44, 0x45, 0x46 ]).
Endianness
All operations are performed on little endian arrays.
This means that if your arbitrary size integer has generic
as_bytes(), to_bytes() or from_bytes() functions, you will need to investigate which endianness it expects and outputs.
To visualize endianness consider the hexadecimal (base/radix 16) number 0xABCD (43981 in decimal (base/radix 10)).
Most hexadecimal string parsers would consider the number to be in big endian representation with the most significant digit A to the far left representing the digit that would affect the number most if changed, in the same way that 1 is the most significant digit in 100 (one hundred).
If you convert the number to big endian bytes the most significant byte, AB, is in the first position and the rest follow along.
In little endian bytes the least significant byte, CD, is the in the first position followed by the second least significant byte, AB in this case.
See the psuedo code below to build a mental model of endianness.
BigInt value = 0xABCD
byte[] big_endian = { 0xAB, 0xCD }
byte[] little_endian = { 0xCD, 0xAB }
To test your BigInt implementation, try to load up the hexadecimal number ABCD and get it as bytes.
The Rust num_bigint library has both to_bytes_le() and to_bytes_be() so there’s no confusion.
Make a note of whether the bytes you get are little endian or big endian.
use num_bigint; // 0.4.0
use num_traits::Num;
fn main() {
let number = num_bigint::BigInt::from_str_radix("ABCD", 16).unwrap();
dbg!(&number.to_bytes_be()); // Outputs [ 171, 205 ] which is [ 0xAB, 0xCD ] in hex
dbg!(&number.to_bytes_le()); // Outputs [ 205, 171 ] which is [ 0xCD, 0xAB ] in hex
}
Remember that there’s a different between the string representation and the literal bytes representation. A hexadecimal string is just a human readable representation of the value, the value of the characters that make up the string is not the same.
Padding
All operations are performed on padded arrays, the sizes for different types can be seen below. Do not worry about understanding why the different sizes are chosen, most are simply the result of the client not being able to accept higher values or having fixed sized fields.
| Type | Size (bytes) | Reason |
|---|---|---|
| Session Key | 40 | Two SHA-1 hashes appended are always 40 bytes. |
| Server and Client Proof | 20 | Result of SHA-1 hash is always 20 bytes. |
| Public Key | 32 | Packet field is always 32 bytes. |
| Private Key | 32 | Arbitrarily chosen. |
| Salt | 32 | Packet field is always 32 bytes. |
| Password Verifier | 32 | Result of modulus large safe prime is always 32 bytes or less. |
| Large Safe Prime | 32 | Largest value client will accept. Any larger can result in public key not fitting into packet field. |
| S Key | 32 | Result of modulus large safe prime is always 32 bytes or less. |
| Reconnect Seed Data | 16 | Packet field is always 16 bytes for both client and server. |
| Generator | 1 | There is no reason to have a generator value above 255. |
Hashing
All operations use SHA-1 which produces an output of 20 bytes.
To test that your SHA-1 implementation works correctly, ensure that hashing the string test leads to the output of a94a8fe5ccb19ba61c4c0873d391e987982fbbd3, and that hashing the bytes 0x53 0x51 leads to 0c3d7a19ac7c627290bf031ec3df76277b0f7f75.
Constants
The large safe prime should always be 0x894B645E89E1535BBDAD5B8B290650530801B18EBFBF5E8FAB3C82872A3E9BB7 (big endian string).
The large safe prime can be expressed as a little endian Rust array like
pub const LARGE_SAFE_PRIME_LITTLE_ENDIAN: [u8; 32] = [
0xb7, 0x9b, 0x3e, 0x2a, 0x87, 0x82, 0x3c, 0xab,
0x8f, 0x5e, 0xbf, 0xbf, 0x8e, 0xb1, 0x01, 0x08,
0x53, 0x50, 0x06, 0x29, 0x8b, 0x5b, 0xad, 0xbd,
0x5b, 0x53, 0xe1, 0x89, 0x5e, 0x64, 0x4b, 0x89
];
or as a big endian Rust array like
pub const LARGE_SAFE_PRIME_BIG_ENDIAN: [u8; 32] = [
0x89, 0x4b, 0x64, 0x5e, 0x89, 0xe1, 0x53, 0x5b,
0xbd, 0xad, 0x5b, 0x8b, 0x29, 0x06, 0x50, 0x53,
0x08, 0x01, 0xb1, 0x8e, 0xbf, 0xbf, 0x5e, 0x8f,
0xab, 0x3c, 0x82, 0x87, 0x2a, 0x3e, 0x9b, 0xb7,
];
The generator should always be 7.
The k value should always be 3.
The XOR Hash with these values will always be 0xA7C27B6C96CA6F505A7C98031173AC383AB07BDD (big endian string).
The XOR Hash can be expressed as a little endian Rust array like
const PRECALCULATED_XOR_HASH: [u8; 20] = [
0xdd, 0x7b, 0xb0, 0x3a, 0x38, 0xac, 0x73, 0x11, 0x3, 0x98,
0x7c, 0x5a, 0x50, 0x6f, 0xca, 0x96, 0x6c, 0x7b, 0xc2, 0xa7,
];
Aliases
Previously terms like client public key and large safe prime have been used instead of the single letters A and N which are used in RFC2945.
The one letter abbreviations are in my opinion difficult to remember and internalize unless you already know what they mean beforehand. The long forms will therefore be used, and the table below will serve as a translation between the long and short forms. Not all terms have a long term, since some terms only exist as intermediate results.
| Short Form | Long Form |
|---|---|
A | Client public key |
a | Client private key |
B | Server public key |
b | Server private key |
N | Large safe prime |
g | Generator |
k | K value |
s | Salt |
U | Username |
p | Password |
v | Password verifier |
M1 | Client proof (proof first sent by client, calculated by both) |
M2 | Server proof (proof first sent by server, calculated by both) |
M | (Client or server) proof |
S | S key |
K | Session key |
Implementation Details
This section describes how to implement the algorithm on a function-by-function basis. A completely functional program will only be possible once everything except for the Reconnect proof has been implemented. Test against the provided text files for every function to ensure that no mistakes occur.
The wow_srp Rust crate implements the full algorithm, with examples for both client and server located in the examples/ directory. WowSrp has a C# version. Ember has a C++ version. Shadowburn has an Elixir version. wow_srp6 is a Python version.
The various Mangos forks and derivatives also have SRP6 implementations but these are of very low quality and some will produce incorrect results in as often as 1/1000 cases.
Password Verifier
The password verifier, v, is calculated as v = g^x % N, where:
gis the static generator equal to 7 defined in Constants.xis discussed below.%is the modulo operator.Nis the static large safe prime defined in Constants.
Calculating the password verifier in pseudo code would look like
function calculate_password_verifier
argument username: string
argument password: string
argument salt: little endian array of 32 bytes
returns little endian array of 32 bytes
x = calculate_x(username, password, salt)
// modpow is a power of and modulo operation in the same function
return g.modpow(x, large_safe_prime)
Implementations
- Rust (wow_srp)
- C# (WowSrp
- C++ (Ember). Slightly confusing way of doing it. Callsite is here, then here and then here.
- Elixir (Shadowburn)
- Python (wow_srp6)
- Go (go-wow-srp6)
Verification values
- calculate_v_values.txt contains the columns:
| Username | Password | Salt | Expected |
|---|---|---|---|
| String | String | Big Endian Hex | Big Endian Hex |
Calculating x
The x value is calculated as x = SHA1( s | SHA1( U | : | p )), where:
Uis the uppercased username of the user. See this section for notes.pis the uppercased password of the user. See this section for notes.sis the randomly generated salt value for the user.|is concatenating the values.SHA1is SHA-1 hashing the values.:is the literal character:.
Calculating x in pseudo code would look like
function calculate_x
argument username: string
argument password: string
argument salt: little endian array of 32 bytes
returns little endian array of 20 bytes
interim = SHA1( username + ":" + password )
// Array concatenation
return SHA1( salt + interim )
Implementations
Verification values
- calculate_x_salt_values.txt assumes a static username of
USERNAME123and a static password ofPASSWORD123. It contains the columns:
| Salt | Expected |
|---|---|
| Big Endian Hex | Big Endian Hex |
- calculate_x_values.txt assumes a static salt of
0xCAC94AF32D817BA64B13F18FDEDEF92AD4ED7EF7AB0E19E9F2AE13C828AEAF57(big endian). It contains the columns:
| Username | Password | Expected |
|---|---|---|
| String | String | Big Endian Hex |
Server public key
The server public key, B, is calculated as B = (k * v + (g^b % N)) % N, where:
kis a k value statically defined in Constants.vis the password verifier for the user.gis a generator statically defined in Constants.bis the server private key.%is the modulo operator.Nis a large safe prime statically defined in Constants.
Calculating the server public key in pseudo code would look like:
function calculate_server_public_key
argument password_verifier: BigInteger type
argument server_private_key: BigInteger type
returns little endian array of 32 bytes
// modpow is a power of and modulo operation in the same function
interim = k_value * password_verifier
+ generator.modpow(server_private_key, large_safe_prime)
return interim % large_safe_prime
Implementations
Verification values
- calculate_B_values.txt contains the columns:
| Password Verifier | Server Private Key | Expected |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
Session key
The session key, K, is calculated differently depending on whether it is the client or server doing the calculation because they only have access to their own private keys.
Both ways calculate an interim S key value that is finally interleaved in order to get the common session key.
For completeness, both the server and client session key, K, is calculated as K = interleaved(S), where interleaved is a function described below.
The calculation of the client and server S keys are below.
Client S Key
The client S Key, S, is calculated as S = (B - (k * (g^x % N)))^(a + u * x) % N, where:
gis a generator statically defined in Constants.%is the modulo operator.Nis a large safe prime statically defined in Constants.kis a k value statically defined in Constants.ais the client private key.Bis the server public key.xis an interim value described under the Password Verifier section.uis an interim value described below.
Calculating the client S key in pseudo code would look like:
function calculate_client_S_key
argument client_private_key: little endian array of 32 bytes
argument server_public_key: little endian array of 32 bytes
argument x: little endian array of 32 bytes
argument u: little endian array of 32 bytes
returns little endian array of 32 bytes
S = (server_public_key - (k * g.modpow(x, large_safe_prime))).modpow(client_private_key + u * x, large_safe_prime)
return S
Implementations
Verification values
If you’re getting an error on the 6th line of this file, your BigInteger implementation is likely using remainder instead of modulo.
- calculate_client_S_values.txt expects a static generator and large safe prime from Constants, and contains the columns:
| Server Public Key | Client Private Key | x | u | Expected |
|---|---|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Server S Key
The server S key, S, is calculated as S = (A * (v^u % N))^b % N, where:
Ais the client public key.vis the password verifier for the user.%is the modulo operator.Nis a large safe prime statically defined in Constants.bis the server private key.uis an interim value described below.
Calculating the server S key in pseudo code would look like:
function calculate_server_S_key
argument client_public_key: BigInteger type
argument password_verifier: BigInteger type
argument u: BigInteger type
argument server_private_key: BigInteger type
returns little endian array of 32 bytes
S = (client_public_key * password_verifier.modpow(u, large_safe_prime))
.modpow(server_private_key, large_safe_prime)
return S
Implementations
Verification values
- calculate_S_values.txt expects a static generator and large safe prime from Constants, and contains the columns:
| Client Public Key | Password Verifier | u | Server Private Key | Expected |
|---|---|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
u
The u value is calculated as u = SHA1( A | B ), where:
Ais the client public key.Bis the server public key.SHA1is SHA-1 hashing.|is array concatenation.
Calculating the server S key in pseudo code would look like:
function calculate_u
argument client_public_key: little endian array of 32 bytes
argument server_public_key: little endian array of 32 bytes
returns little endian array of 20 bytes
return SHA1( A + B )
Implementations
- Rust (wow_srp)
- C# (WowSrp
- C++ (Ember)
- Elixir (Shadowburn) where it’s called the scrambler.
- Python (wow_srp6)
- Go (go-wow-srp6)
Verification values
- calculate_u_values.txt contains the columns:
| Client Public Key | Server Public Key | Expected |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
Interleaved
The interleaved function converts the S key to the session key.
It is calculated as K = SHA_Interleave(S), where:
Kis the session key.Sis the S key.SHA_Interleave()is a function described below:
If the least significant byte is 0, the two least significant bytes are removed. If the next least significant byte is also 0, the two new least significant bytes are again removed. This process continues until the least significant byte is not equal to 0. The even elements of the split S key are then hashed, as are the odd elements. The two hashes are then zipped together, with the even elements in the first position.
The SHA_Interleave() function in pseudo code would look like:
function split_s_key
argument s_key: little endian array of 32 bytes
returns little endian array of 32 bytes or fewer
// While the _least_ significant byte is 0,
// remove the 2 least significant bytes.
// Always keep the length even without
// trailing zero elements
while s_key[0] == 0
// In the pseudo code the s_key variable is modified in place
// so the first iteration `s_key` has length 32, in the second
// it has length 30, and so on.
s_key = s_key[2:]
return s_key
function SHA_Interleave
argument s_key: little endian array of 32 bytes
returns array of 40 bytes
split_s_key = split_s_key(s_key)
E = dynamic vector of bytes
// Only add the even elements
for i in split_s_key.even_elements
E.push(i)
G = SHA1(E)
F = dynamic vector of bytes
for i in split_s_key.odd_elements
F.push(i)
H = SHA1(F)
session_key = little endian array of 40 bytes
for i = 0, while i < 20, i += 2
session_key[i * 2] = G[i]
session_key[(i * 2) + 1] = H[i]
return session_key
Implementations
- Rust (wow_srp) (
split_s_key) - Rust (wow_srp)
- C# (WowSrp (
SplitSKey) - C# (WowSrp
- C++ (Ember)
- Elixir (Shadowburn)
- Python (wow_srp6)
- Go (go-wow-srp6)
Verification values
- calculate_interleaved_values.txt contains the columns:
| S Key | Expected |
|---|---|
| Big Endian Hex | Big Endian Hex |
- calculate_split_s_key.txt contains the columns:
| S Key | Expected |
|---|---|
| Big Endian Hex | Big Endian Hex |
Server Session Key
The server session key combines all the previous functions:
function calculate_server_session_key:
argument client_public_key: array of 32 bytes
argument server_public_key: array of 32 bytes
argument password_verifier: array of 32 bytes
argument server_private_key: array of 32 bytes
returns array of 40 bytes
u = calculate_u(client_public_key, server_public_key)
S = calculate_S(client_public_key, password_verifier, u, server_private_key)
return calculate_interleaved(S)
}
Implementations
Verification values
You will need to calculate the server public key using the supplied password verifier and server private key in order to test this.
- calculate_server_session_key.txt contains the columns:
| Client Public Key | Password Verifier | Server Private Key | Expected |
|---|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Client Session Key
The client session key combines all the previous functions:
function calculate_client_session_key:
argument username: string
argument password: string
argument server_public_key: array of 32 bytes
argument client_private_key: array of 32 bytes
argument generator: unsigned integer
argument large_safe_prime: array of 32 bytes
argument client_public_key: array of 32 bytes
argument salt: array of 32 bytes
returns array of 40 bytes
x = calculate_x(username, password, salt)
u = calculate_u(client_public_key, server_public_key)
S = calculate_client_S(
server_public_key,
x,
client_private_key,
u,
generator,
large_safe_prime,
)
return calculate_interleaved(S)
}
Implementations
Verification values
- calculate_client_session_key.txt contains the columns:
| Username | Password | Server Public Key | Client Private Key | Generator | Large Safe Prime | Client Public Key | Salt | Expected |
|---|---|---|---|---|---|---|---|---|
| String | String | Big Endian Hex | Big Endian Hex | Integer | Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Server proof
The server proof, M2 or sometimes just M, is calculated as M2 = SHA1(A | M1 | K), where:
Ais the client public key.M1is the client proof. Remember thatM1must be calculated and verified on the server before this calculation takes place.Kis the session key.|is concatenation.
Calculating the server proof in pseudo code would look like:
function calculate_server_proof
argument client_public_key: little endian array of 32 bytes
argument client_proof: little endian array of 20 bytes
argument session_key: little endian array of 40 bytes
returns little endian array of 20 bytes (SHA1 hash)
// Array concatenation
return SHA1(client_public_key + client_proof + session_key)
Implementations
- Rust (wow_srp)
- C# (WowSrp
- C++ (Ember) calls into here.
- Elixir (Shadowburn)
- Python (wow_srp6)
- Go (go-wow-srp6)
Verification values
- calculate_M2_values.txt contains the columns:
| Client Public Key | Client Proof | Session Key | Expected |
|---|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Client proof
The client proof, M1 or sometimes just M, is calculated as M1 = SHA1( X | SHA1(U) | s | A | B | K ), where:
Xis theXOR Hash, described below. It requires the large safe prime and the generator. Can be precalculated if both are known.SHA1(U)is a SHA-1 hash of the uppercased username.sis the salt.Ais the client public key.Bis the server public key.Kis the session key.
Calculating the client proof in pseudo code would look like:
function calculate_client_proof
argument xor_hash: little endian array of 20 bytes
argument username: string
argument session_key: little endian array of 40 bytes
argument client_public_key: little endian array of 32 bytes
argument server_public_key: little endian array of 32 bytes
argument salt: little endian array of 32 bytes
hashed_username = SHA1( username )
// | is array concatenation
return SHA1( xor_hash
| hashed_username
| salt
| client_public_key
| server_public_key
| session_key )
Implementations
Verification values
- calculate_M1_values.txt contains the columns:
| Username | Session Key | Client Public Key | Server Public Key | Salt | Expected |
|---|---|---|---|---|---|
| String | Big endian hex | Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
XOR Hash
This value can be precalculated on the server and you can avoid the calculation. See the verification values for the value.
The xor_hash is calculated as SHA1(N) XOR SHA1(g), where:
SHA1(g)is a SHA-1 hash of the generator statically defined in Constants on the server and variable on the client.SHA1(N)is a SHA-1 hash of the large safe prime statically defined in Constants on the server and variable on the client.XORuses the XOR operator on every element of the two arrays.
Calculating the XOR Hash in pseudo code would look like:
function calculate_xor_hash
argument large_safe_prime: little endian array of 32 bytes
argument generator: byte value
returns little endian array of 20 bytes (SHA-1 hash)
hashed_generator = SHA1( generator )
hashed_large_safe_prime = SHA1( large_safe_prime )
result is a 20 byte array
for index in hashed_generator
result[index] = hashed_generator[index] ^ hashed_large_safe_prime[index]
end for
return result
Implementations
Verification values
- calculate_xor_hash.txt contains the columns:
| Generator | Large Safe Prime | Client Public Key |
|---|---|---|
| Decimal Number | Big endian hex | Big Endian Hex |
Client public key
Generating the client public key is not necessary if you’re only writing the server part.
The client public key, A, is calculated as A = g^a % N, where:
gis a generator. Clients do not get to choose the generator, so they can not assume a static value is used.ais the client private key.%is the modulo operator.Nis a large safe prime. Clients do not get to choose the large safe prime, so they can not assume a static value is used.
Calculating the client public key in pseudo code would look like:
function calculate_client_public_key
argument client_private_key: little endian array of 32 bytes
argument generator: 1 byte integer
argument large_safe_prime: little endian array of 32 bytes
returns little endian array of 32 bytes
// modpow is a power of and modulo operation in the same function
return generator.modpow(client_private_key, large_safe_prime)
Implementations
Verification values
- calculate_A_values.txt expects a static generator and large safe prime as defined under Constants. It contains the columns:
| Client Private Key | Expected |
|---|---|
| Big Endian Hex | Big Endian Hex |
Reconnecting
If a client loses connection with the logon server after getting a session key but before connecting to a realm, the client will attempt bypass the creation of a new session key by proving to the client that it knows the old session key.
When reconnecting, the protocol works in 6 steps:
- The client sends their username to the server.
- The server checks for an existing session with the username and creates randomized server data that it sends to the client.
- The client generates randomized client data and uses the server data along with the username and session key to create a reconnect proof. It then sends the client data and reconnect proof to the server.
- The server calculates their own reconnect proof from the username, server data, client data, and session key to see if it matches the client reconnect proof.
- The client is now authenticated again and will send the ‘Send Realmlist’ packet to as the server to send a realmlist.
The above description can also be seen as a sequence diagram in figure 2.
PlantUML Source
The only function needed for the above is calculating the reconnect proof and generating random 16 byte values.
Reconnect proof
The reconnect proof is not part of SRP6 and does not have a short term. It is calculated the same for the client and server.
The reconnect proof is calculated as SHA1( username | client_data | server_data | session_key ), where:
usernameis the username of the user attempting to reconnect.client_datais the randomized data sent by the client.server_datais the randomized data sent by the server.session_keyis the session key from a previous successful authentication.|is array concatenation. Strings are converted to UTF-8 bytes.
Calculating the client public key in pseudo code would look like:
function calculate_reconnect_proof
argument username: string
argument client_data: little endian array of 16 bytes
argument server_data: little endian array of 16 bytes
argument session_key: little endian array of 40 bytes
returns little endian array of 20 bytes
return SHA1(username + client_data + server_data + session_key)
Implementations
Verification values
- calculate_reconnection_values.txt contains the columns:
| Username | Client Data | Server Data | Session Key | Expected |
|---|---|---|---|---|
| String | Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
Vanilla World Message Header Encryption
World Packets encrypt their header using the session key. None of the Login Packets require encryption, but this section is included because it can be tedious to implement and is necessary for getting to the character screen.
The sending party encrypts the header and the receiving party decrypts the header. Client and server headers have different length, but this does not matter since the algorithm works on any amount of bytes.
The “encryption” is not real encryption, since it’s very easily breakable and can leak the session key which is used for reconnection.
To be explicit, if you’re writing a server you will only ever decrypt headers received from the client and encrypt headers sent to the client.
Figure 3 shows both encryption and decryption visually. Individual images can be found at step 1, step 2, step 3, step 4 and step 5.
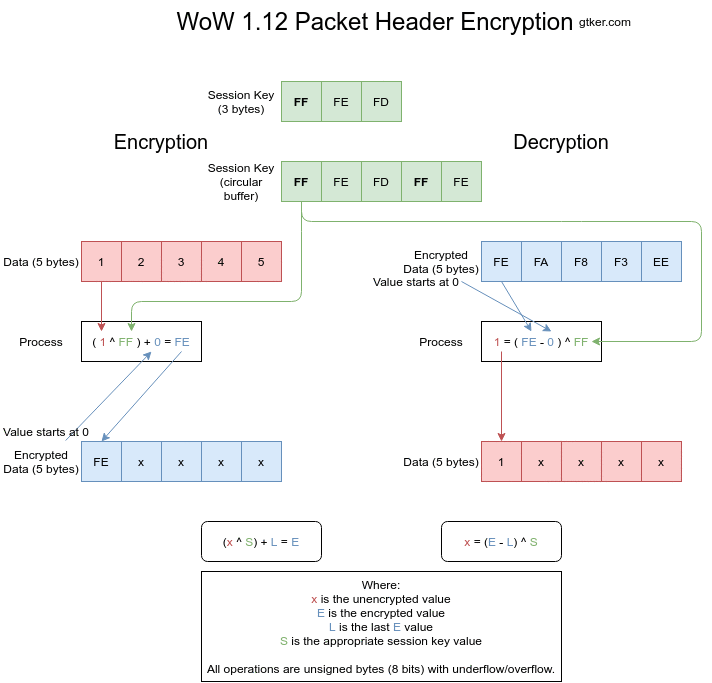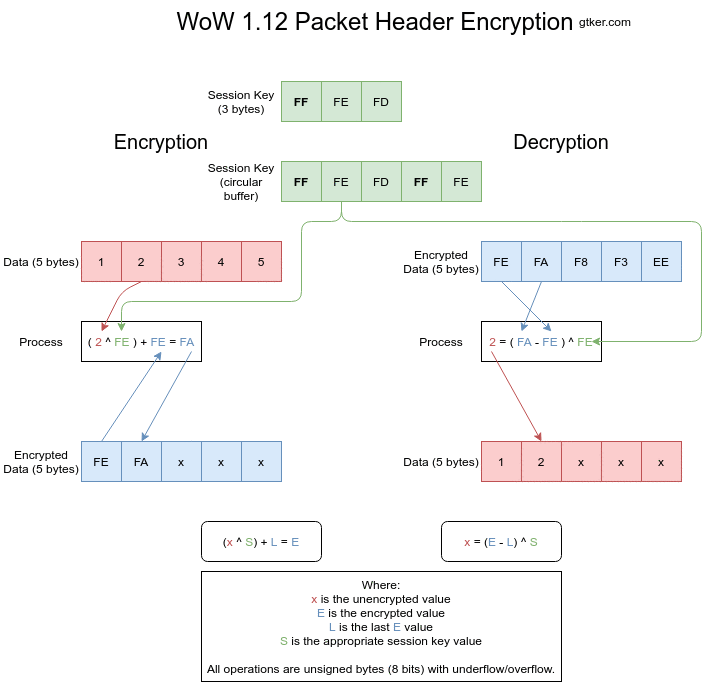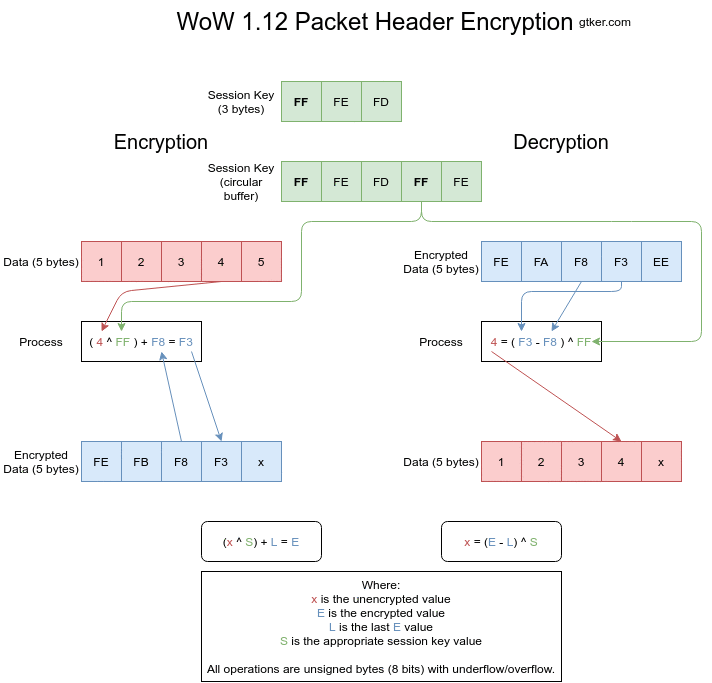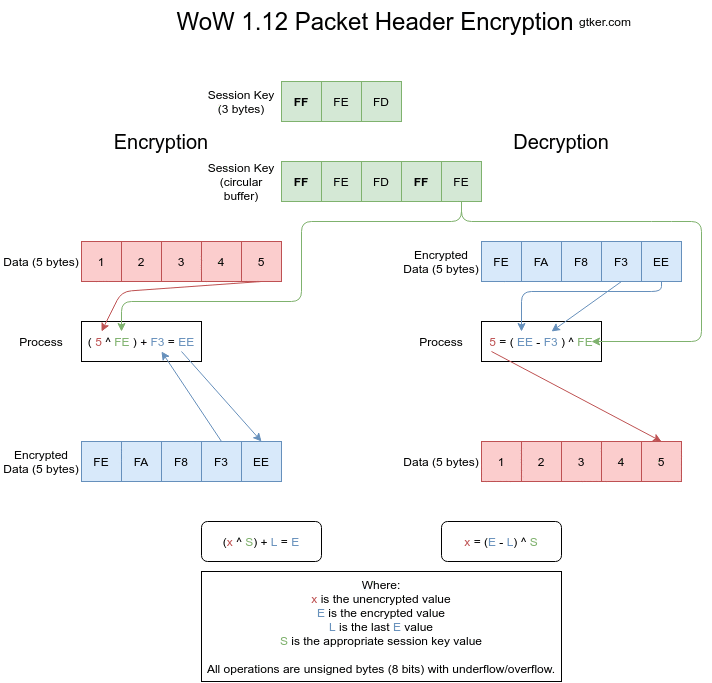
Encryption
Encryption works by XORing the unencrypted value with a byte of the session key and adding the previous encrypted value. The index into the session key is then incremented. This is done for every element of the array to be encrypted.
The encryption is calculated as E = (x ^ S) + L where:
Eis the encrypted value, what is sent over the wire.xis the unencrypted value, a byte of the opcode or size.Sis a byte of the session key, incrementing after every encryption.Lis the last encrypted value. This isEfrom the previous iteration.
In pseudo code this would look like:
function encrypt
argument data: little endian array of length AL
returns little endian array of length AL
static int index = 0 // Static variables keep their values between function calls
static int last_value = 0 // Last value starts at zero
// The session key exists somewhere else as `session_key`
return_array = {} // Encrypted values
for unencrypted in data {
encrypted = (unencrypted ^ session_key[index]) + last_value
index = (index + 1) % session_key.length // Use the session key as a circular buffer
return_array.append(encrypted)
last_value = encrypted
}
return return_array
Implementations
Verification values
- calculate_encrypt_values.txt contains the columns:
| Session Key | Data (50 bytes) | Expected (50 bytes) |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
The following files can be used to verify utility methods that return a size and opcode. The data should be decrypted first using the side in the file name, then encrypted again in order to verify that the write also matches.
session_key = [
0x2E, 0xFE, 0xE7, 0xB0, 0xC1, 0x77, 0xEB, 0xBD, 0xFF, 0x66, 0x76, 0xC5, 0x6E, 0xFC, 0x23,
0x39, 0xBE, 0x9C, 0xAD, 0x14, 0xBF, 0x8B, 0x54, 0xBB, 0x5A, 0x86, 0xFB, 0xF8, 0x1F, 0x6D,
0x42, 0x4A, 0xA2, 0x3C, 0xC9, 0xA3, 0x14, 0x9F, 0xB1, 0x75,
];
username = "A";
client_seed = 0xDEADBEEF;
server_seed = 0xDEADBEEF;
- vanilla_server contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
- vanilla_client contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
Decryption
Decryption does the opposite of encryption. So first the old encrypted value is subtracted from the encrypted value, before it is XORed with the session key.
The decryption is calculated as x = (E - L) ^ S where:
xis the unencrypted value, a byte of the opcode or size.Eis the encrypted value, what is sent over the wire.Lis the last encrypted value. This isEfrom the previous iteration.Sis a byte of the session key, incrementing after every encryption.
In pseudo code this would look like:
function decrypt
argument data: little endian array of length AL
returns little endian array of length AL
static int index = 0 // Static variables keep their values between function calls
static int last_value = 0 // Last value starts at zero
// The session key exists somewhere else as `session_key`
return_array = {} // Unencrypted values
for encrypted in data {
unencrypted = (encrypted - last_value) ^ session_key[index]
index = (index + 1) % session_key.length // Use the session key as a circular buffer
last_value = encrypted
return_array.append(unencrypted)
}
return return_array
Implementations
Verification values
- calculate_decrypt_values.txt contains the columns:
| Session Key | Data (50 bytes) | Expected (50 bytes) |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
TBC World Message Header Encryption
Has the same implementation for encryption/decryption as Vanilla, but it performs an HMAC-SHA1 on the session key along with a seed and iterates over that instead. Verification values are provided for
Remember that the key for TBC is only 20 bytes, while it’s 40 for Vanilla so you will probably need different functions for each.
Key Generation
HMAC-SHA1is the HMAC-SHA1 function.
In pseudo code the generation looks like:
function create_tbc_key:
argument session_key: array of 40 bytes
returns array of 20 bytes
S = [0x38, 0xA7, 0x83, 0x15, 0xF8, 0x92, 0x25, 0x30, 0x71, 0x98, 0x67, 0xB1, 0x8C, 0x4, 0xE2,
0xAA]
hmac = HMAC-SHA1(S)
hmac.update(session_key)
return hmac.finalize()
Implementations
Verification values
- create_tbc_key.txt contains the columns:
| Session Key | Expected |
|---|---|
| Big Endian Hex | Big Endian Hex |
Encryption/Decryption
This is identical to the Vanilla version except the key is only 20 bytes instead of 40 bytes.
Encrypt this and verify that it matches Expected Encrypt, then decrypt it and verify that it matches the original Data.
Verification values
- calculate_tbc_encrypt_values.txt contains the columns:
| Session Key | Data | Expected Encrypt |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
The following files can be used to verify utility methods that return a size and opcode. The data should be decrypted first using the side in the file name, then encrypted again in order to verify that the write also matches.
session_key = [
0x2E, 0xFE, 0xE7, 0xB0, 0xC1, 0x77, 0xEB, 0xBD, 0xFF, 0x66, 0x76, 0xC5, 0x6E, 0xFC, 0x23,
0x39, 0xBE, 0x9C, 0xAD, 0x14, 0xBF, 0x8B, 0x54, 0xBB, 0x5A, 0x86, 0xFB, 0xF8, 0x1F, 0x6D,
0x42, 0x4A, 0xA2, 0x3C, 0xC9, 0xA3, 0x14, 0x9F, 0xB1, 0x75,
];
username = "A";
client_seed = 0xDEADBEEF;
server_seed = 0xDEADBEEF;
- tbc_server contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
- tbc_client contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
Wrath World Message Header Encryption
Wrath creates an intermediate key by running a fixed key and the session key through HMAC-SHA1, and then uses this to seed an RC4A cipher that encrypts the header.
The key generation function is essentially the same as the TBC generation, except TBC uses the same hardcoded seed for both client and server, while Wrath has separate keys.
The seed keys are:
// Used for Client (Encryption) to Server (Decryption)
const S: [u8; 16] = [
0xC2, 0xB3, 0x72, 0x3C, 0xC6, 0xAE, 0xD9, 0xB5, 0x34, 0x3C, 0x53, 0xEE, 0x2F, 0x43, 0x67, 0xCE,
];
// Used for Server (Encryption) to Client (Decryption) messages
const R: [u8; 16] = [
0xCC, 0x98, 0xAE, 0x04, 0xE8, 0x97, 0xEA, 0xCA, 0x12, 0xDD, 0xC0, 0x93, 0x42, 0x91, 0x53, 0x57,
];
Key Generation
HMAC-SHA1is the HMAC-SHA1 function.
In pseudo code the generation looks like:
function create_wrath_key:
argument session_key: array of 40 bytes
argument key: array of 16 bytes
returns array of 20 bytes
hmac = HMAC-SHA1(key)
hmac.update(session_key)
return hmac.finalize()
Implementations
Verification values
- create_wrath_hmac_key.txt contains the columns:
| Session Key | Key | Expected |
|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex |
Encryption/Decryption
Initialize a RC4A with the previously calculated key. Then apply the keystream to 1024 bytes (since this is the drop1024 variant).
After this apply the keystream to the header to be encrypted.
function create_crypto:
argument session_key: array of 40 bytes
argument key: array of 16 bytes
returns RC4A in progress
S = create_wrath_key(session_key, key)
rc4 = RC4(S)
rc4.apply_keystream to 1024 0 bytes
retrurn rc4
function encrypt/decrypt:
argument rc4: RC4A in progress
argument data: array of bytes
# Modifies data in place
rc4.apply(data)
Implementations
Verification values
These verification values use the above keys. Ensure that you’re using the correct one for the correct direction and side.
- calculate_wrath_encrypt_values.txt contains the columns:
| Session Key | Data | Expected Client Encrypt | Expected Server Encrypt | |
|---|---|---|---|---|
| Big Endian Hex | Big Endian Hex | Big Endian Hex | Big Endian Hex |
The following files can be used to verify utility methods that return a size and opcode. The data should be decrypted first using the side in the file name, then encrypted again in order to verify that the write also matches.
session_key = [
0x2E, 0xFE, 0xE7, 0xB0, 0xC1, 0x77, 0xEB, 0xBD, 0xFF, 0x66, 0x76, 0xC5, 0x6E, 0xFC, 0x23,
0x39, 0xBE, 0x9C, 0xAD, 0x14, 0xBF, 0x8B, 0x54, 0xBB, 0x5A, 0x86, 0xFB, 0xF8, 0x1F, 0x6D,
0x42, 0x4A, 0xA2, 0x3C, 0xC9, 0xA3, 0x14, 0x9F, 0xB1, 0x75,
];
username = "A";
client_seed = 0xDEADBEEF;
server_seed = 0xDEADBEEF;
- wrath_server contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
- wrath_client contains the columns:
| Data (8 bytes) | Size | Opcode |
|---|---|---|
| Big Endian Hex | Unsigned Integer | Unsigned |
World Server Proof
After receiving the CMSG_AUTH_SESSION
wiki
message the server will have to verify that the client does indeed know the correct session key. This is done by having both the server and client use 32 bit (not byte) values as seeds in a hash with the session key.
The world server proof works for all versions from Vanilla through to Wrath.
The proof is calculated as SHA1( username | 0 | client_seed | server_seed | session_key ), where:
usernameis the username of the user attempting to connect.0is the literal value zero, taking up 4 bytes (32 bits, a standardint).client_seedis a random 4 byte value sent by the client.server_seedis a random 4 byte value generated by the server.session_keyis the session key from the original authentication.
Calculating the world proof in pseudo code would look like:
function calculate_world_server_proof
argument username: string
argument client_seed: unsigned 4 byte value, converted to little endian bytes
argument server_seed: unsigned 4 byte value, converted to little endian bytes
argument session_key: little endian array of 40 bytes
returns little endian array of 20 bytes
zero = [0, 0, 0, 0] // Assume this is a 4 byte array of zeros
return SHA1(username + zero + client_seed + server_seed + session_key)
Implementations
- Rust (wow_srp)
- C# (WowSrp)
- C++ (Ember)
- C++ (Mangos)
- Elixir (Shadowburn)
- Python (wow_srp6)
- Go (go-wow-srp6)
Verification values
- calculate_world_server_proof.txt contains the columns:
| Username | Session Key | Server Seed | Client Seed | Expected |
|---|---|---|---|---|
| String | Big Endian Hex | Number | Number | Big Endian Hex |
Notes on uppercasing username and password
The username and password are UTF-8 strings that are automatically uppercased by the client before being sent over the network. This might present some issues with getting the correct name from the registration form and the client, more information is present at the wow_srp library documentation.
External Resources
- The Shadowburn Project has a guide on authenticating that focuses more on the networking and specific packets.
- The WoWDev Wiki has an overview of packets.
- Wireshark at version 3.5 or greater has support for parsing 1.12 packets through the
WOWandWOWWprotocols. You will need this if you’re trying to debug a networked implementation.