World of Warcraft versions after 2.0.1.6180 supports using Matrix Cards/Grid Cards as multi factor authentication during login.
Matrix Cards are a form of Pre-shared Key where the client is tested on partial elements of the shared key on every login.
This post details how the implementation works and how to use it.
Background
Matrix Cards are a relatively niche form of two factor authentication where the client is tested on partial elements of a Pre-shared Key. The client is first given a Matrix Card in the form of either a document or a physical card akin to the one shown in figure 1.
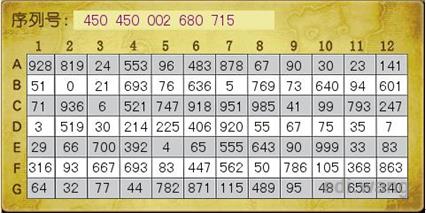
The Chinese text in the top left means “Serial Number:”. This card is very unlikely to have been used with the Wrath of the Lich King or prior clients since it has a variable number of digits per field, which this algorithm does not support, however it can still be used to illustrate how the system works.
The server would ask the client which digits are in cell “A6” and the client would enter “483”. This would repeat for however many rounds the server has requested. The results are then hashed and the proof is sent by the client. The server makes the same calculations and compares the hashes. If they are identical the client knows the layout of the Matrix Card.
The server may send a width, height, digit count, challenge count, and seed in CMD_AUTH_LOGON_CHALLENGE_Server
wiki
.
The client may send the resulting proof in CMD_AUTH_LOGON_PROOF_Client
wiki
.
Real clients will always reply with a proof if the fields from the server message are present.
If the server also sends the fields required for PIN authentication the PIN prompt will be displayed first, followed by the Matrix Card prompt.
Figure 2 shows the complete login process in a 3.3.5 client with Matrix Card validation with a width of 10 and height of 20, digit count of 3, and challenge count of 2.
Implementation details
This section describes how to implement the algorithm on a function-by-function basis. A completelely functional program will only be possible when everything has been implemented.
The wow_srp Rust crate implements the full algorithm. This Github Gist by Barncastle implements the full algorithm in C#.
The algorithm requires keeping the state of in progress RC4 and HMAC-SHA1 objects alive while the algorithm is executed.
Generate Coordinates
The coordinates control which fields are checked.
widthis the width sent by the server.heightis the height sent by the server.challenge_countis the challenge count/rounds sent by the server.seedis the seed sent by the server.%is the modulus operator.
Generating the coordinate array in pseudo code:
function generate_coordinates
argument width: u8
argument height: u8
argument challenge_count: u8
argument seed: u64
returns array of u32s
# width, height, and challenge_count can not be 0
# challenge_count must be greater than or equal to width * height
matrix_indices = array of (width * height) u32s that where the value is the same as the index
# So if width * height was 4 the matrix_indices would be [0, 1, 2, 3]
coordinates = array of challenge_count u32s
for i, coordinate in enumerate(coordinates):
count = len(matrix_indices) - i;
index = seed % count;
coordinate = matrix_indices[index];
for j in index..(count - 1) {
matrix_indices[j] = matrix_indices[j + 1];
}
seed /= count;
return coordinates
Implementations
Verification values
coordinates_regressioncontains the columns:
width | height | challenge_count | seed | expected |
|---|---|---|---|---|
| unsigned integer | unsigned integer | unsigned integer | unsigned integer | challenge_count amount of space separated unsigned integers |
Create new objects
This function creates the coordinates, rc4, and hmac objects required for further functions.
widthis the width sent by the server.heightis the height sent by the server.challenge_countis the challenge count/rounds sent by the server.seedis the seed sent by the server.session_keyis the 40 byte session key created by the SRP6 algorithm.MD5is the MD5 hash function.HMAC-SHA1is the HMAC-SHA1 function.RC4is the RC4 function.+is array concatenation
Creating the objects in pseudo code:
function create_new_objects
argument width: u8
argument height: u8
argument challenge_count: u8
argument seed: u64
argument session_key: array of 40 bytes
returns in-progress HMAC-SHA1, in-progress RC4, array of u32s
coordinates = generate_coordinates(width, height, challenge_count, seed)
md5 = MD5(seed as little endian array + session_key)
# Do not drop anything, unlike headers dropping 1024
rc4 = RC4(md5)
hmac = HMAC-SHA1(md5)
return hmac, rc4, coordinates
Implementations
Verification values
There are no verification values for this function since the HMAC and RC4 ciphers aren’t finished, and the coordinates are verified in Generate Coordinates.
Get Coordinate
This function returns the (x, y) location on the pre shared key that should be entered using Enter Value.
widthis the width sent by the server.heightis the height sent by the server.challenge_countis the challenge count/rounds sent by the server.roundis the iteration number. So the first iteration would be 0, the second 1, and so on.coordinatesis the array created by Generate Coordinates.
Getting coordinates in pseudo code would look like:
function get_coordinate
argument challenge_count: u8
argument coordinates: array of u32s
argument width: u8
argument height: u8
argument round: u8
returns u8, u8
# round can not be greater than challenge_count
coord = coordinates[round]
x = coord % width
y = coord / width
# y can not be greater than or equal to height
return x, y
Implementations
Verification Values
get_coordinate_regressioncontains the columns:
height | width | seed | challenge_count | session_key | expected |
|---|---|---|---|---|---|
| unsigned integer | unsigned integer | unsigned integer | unsigned integer | Big endian array | challenge_count pairs of x and y separated by space |
Enter Digit
Enters a single digit from a cell.
Digits should be in the range [0;9] and should be entered one by one.
Nothing needs to be done in between rounds.
Entering digits in pseudo code would look like:
function enter_digit
argument rc4: in progress RC4 object created by create_new_objects
argument hmac: in progress HMAC-SHA1 object created by create_new_objects
argument value: u8
new_value = rc4.apply(value)
hmac.apply(new_value)
Implementations
Verification Values
Since this function doesn’t provide any output there are no verification values. Test this using Create Proof instead.
Create Proof
Finalizes the proof after digits have been entered.
In pseudo code it would look like:
function create_proof
argument hmac: in progress HMAC-SHA1 object created by create_new_objects
returns array of 20 bytes
return hmac.finalize()
Implementations
Verification Values
proof_regressioncontains the columns:
height | width | seed | session_key | expected | challenge_count | challenges |
|---|---|---|---|---|---|---|
| unsigned integer | unsigned integer | unsigned integer | Big endian array | Big endian array | unsigned integer | challenge_count unsigned integers to be entered using Enter Digit |
Usage
Usage in pseudo code would look like:
width = 26
height = 26
challenge_count = 2
digit_count = 3
seed = random()
session_key = a valid generated session key
hmac, rc4, coordinates = create_new_objects(width, height, challenge_count, seed, session_key)
for round in 0..challenge_count:
x, y = get_coordinate(challenge_count, coordinates, width, height, round)
digits = use x and y to get the cell digits
for digit in digits:
value = enter_digit(rc4, hmac, digit)
create_proof(hmac)
# Send the proof to the server, or compare it with what the client sent